Lãi kép – Wikipedia tiếng Việt

0 Shares

Lãi kép phát sinh khi phần lãi vừa đạt được được thêm vào vốn ban đầu, do đó, từ thời điểm đó trở đi, lãi phát sinh được tính dựa trên tổng của vốn ban đầu và số tiền lãi vừa kiếm được. Sự bổ sung tiền lãi vào vốn ban đầu được gọi là tính lãi kép hay nhập vốn.

Một thông tin tài khoản ngân hàng nhà nước, Thí dụ, hoàn toàn có thể có lãi kép hàng năm : trong trường hợp này, một thông tin tài khoản với 1000 đô-la tiền vốn gốc khởi đầu và lãi suất vay 20 % mỗi năm sẽ có số dư 1200 đô-la vào cuối năm tiên phong, 1440 đô-la vào cuối năm thứ hai, và cứ như vậy .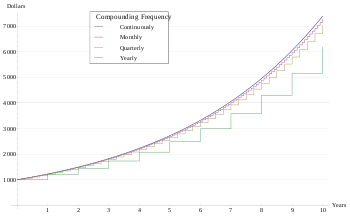

Hiệu quả của việc hưởng tiền lãi hàng năm 20% trên một đầu tư ban đầu 1.000 đô-la với các tần suất tính lãi kép khác nhau

Bạn đang đọc: Lãi kép – Wikipedia tiếng Việt

Bạn đang đọc: Lãi kép – Wikipedia tiếng Việt

Để xác định một lãi suất đầy đủ, và cho phép so sánh nó với các lãi suất khác, lãi suấtvàtần suất tính lãi kép phải được cung cấp. Vì hầu hết mọi người thích nghĩ về lãi suất này như là một tỷ lệ phần trăm hàng năm, nhiều chính phủ yêu cầu các tổ chức tài chính cung cấp mức lãi suất kép hàng năm tương đương trên tiền gửi hoặc tiền ứng trước.

Thí dụ, lãi suất vay hàng năm cho một khoản vay với lãi vay 1 % mỗi tháng là khoảng chừng 12,68 % một năm ( 1.0112 − 1 ) .

Lãi suất hàng năm tương đương này có thể được gọi là tỷ lệ phần trăm hàng năm (APR), lãi suất tương đương hàng năm (AER), lãi suất hiệu quả, lãi suất hàng năm hiệu quả, và các thuật ngữ khác. Khi một khoản phí đã được tính trước để có được một khoản vay, APR thường tính rằng chi phí cũng như lãi kép trong việc chuyển đổi sang lãi suất tương đương. các yêu cầu chính phủ này hỗ trợ người tiêu dùng để so sánh chi phí thực tế của khoản vay dễ dàng hơn.

Đối với bất kỳ lãi suất nhất định và tần suất kép nào, đều có một lãi suất “tương đương” cho một tần suất kép khác nào đó tồn tại.[cần dẫn nguồn]

Lãi kép hoàn toàn có thể được so sánh với lãi đơn, trong đó tiền lãi không được nhập tiền gốc ( không có lãi kép ). Lãi kép là tiêu chuẩn trong kinh tế tài chính và kinh tế tài chính, và lãi đơn được dùng liên tục ( mặc dầu các loại sản phẩm kinh tế tài chính nhất định hoàn toàn có thể chứa các thành phần của lãi đơn ) .

Tác động của việc tính lãi kép phụ thuộc vào tần suất mà tiền lãi được tính lãi kép và lãi suất định kỳ được áp dụng. Vì vậy, để xác định chính xác số tiền phải trả theo hợp đồng pháp lý với tiền lãi, tần suất tính lãi kép (hàng năm, nửa năm, hàng quý, hàng tháng, hàng ngày, vv) và lãi suất phải được xác định. Các quy ước khác nhau có thể được dùng giữa các nước, nhưng trong tài chính và kinh tế học các tập quán sau đây là phổ biến:

Lãi suất định kỳ : tiền lãi mà được tính phí ( và được hợp gốc sau đó ) cho từng quy trình tiến độ, chia cho số tiền gốc. Lãi suất định kỳ được dùng đa phần cho các thống kê giám sát, và hiếm khi được dùng để so sánh .Lãi suất danh nghĩa hàng năm hoặc lãi suất vay danh nghĩa được định nghĩa là lãi suất vay định kỳ nhân với số thời kỳ tính lãi kép mỗi năm. Thí dụ, một lãi suất vay hàng tháng là 1 % tương tự với lãi suất vay danh nghĩa hàng năm là 12 % .Lãi suất hàng năm hiệu suất cao : điều này phản ánh lãi suất vay này hiệu suất cao như nếu việc tính lãi kép hàng năm được vận dụng : nói phương pháp khác, nó là tổng số tiền lãi cộng dồn mà hoàn toàn có thể được trả đến cuối của một năm, chia cho số tiền gốc .Các nhà kinh tế tài chính thường thích dùng lãi suất vay hàng năm hiệu suất cao để cho phép so sánh. Trong kinh tế tài chính và thương mại, lãi suất vay hàng năm danh nghĩa Tuy vậy hoàn toàn có thể là một trích dẫn thay thế sửa chữa. Khi trích dẫn cùng với tần suất tính lãi kép, một khoản vay với lãi suất vay hàng năm danh nghĩa đã cho được xác lập khá đầy đủ ( ảnh hưởng tác động của tiền lãi suất vay so với một ngữ cảnh cho vay đơn cử hoàn toàn có thể được xác lập đúng mực ), nhưng lãi suất vay danh nghĩa không hề được so sánh trực tiếp với các khoản vay có tần suất tính lãi kép khác nhau .Các khoản vay và hỗ trợ vốn hoàn toàn có thể có các tính phí ” không lãi ” khác, và các thuật ngữ trên không cố gắng nỗ lực để chớp lấy các sự khác lạ này. Các thuật ngữ khác như tỷ suất Phần Trăm hàng năm và lợi suất Xác Suất hàng năm hoàn toàn có thể có các định nghĩa hợp pháp đơn cử và hoàn toàn có thể hoặc không hề được so sánh, tùy thuộc vào thẩm quyền .Việc dùng các thuật ngữ trên ( và các thuật ngữ tương tự như khác ) hoàn toàn có thể là không tương thích, và đổi khác theo tùy chỉnh địa phương hoặc nhu yếu tiếp thị, cho đơn thuần hoặc vì các nguyên do khác .

Các ngoại lệ

Tín phiếu T của Mỹ và Canada (nợ Chính phủ ngắn hạn) có một quy ước khác. Tiền lãi của chúng được tính là (100 − P)/ Pbnm, ở đây P là giá thanh toán. Thay vì bình thường hóa nó cho một năm, tiền lãi được tính tỷ lệ theo số ngày t: (365/t)×100. (Xem quy ước tính ngày).Lãi vay trên trái phiếu doanh nghiệp và trái phiếu chính phủ thường phải trả hai lần mỗi năm. Số tiền lãi thanh toán (mỗi sáu tháng) là lãi suất công bố chia cho hai (nhân với số tiền gốc). Lãi suất gộp hàng năm là cao hơn mức công bố.Các cho vay thế chấp Canada nói chung là tính lãi kép nửa năm với các khoản thanh toán hàng tháng (hoặc thường xuyên hơn).Các cho vay thế chấp Mỹ dùng một cho vay trả góp, tiền lãi không tính kép. Với các khoản vay này, một lịch trình trả góp được dùng để xác định phương pháp áp dụng các thanh toán đối với số tiền gốc và lãi vay. Tiền lãi tạo ra trên các khoản vay này không được thêm vào số tiền gốc, nhưng thay vào đó được trả hết hàng tháng như các thanh toán được áp dụng.Nó là đôi khi đơn giản toán học, Thí dụ trong định giá trị các phái sinh để dùng lãi kép liên tục, đó là giới hạn khi số thời kỳ tính lãi kép tiến tới không. Việc tính lãi kép liên tục trong định giá các công cụ này là một hệ quả tự nhiên của tính toán Itō, trong đó các phái sinh có giá trị ở tần suất ngày càng tăng, cho đến khi giới hạn được tiếp cận và phái sinh có giá trị trong thời gian liên tục.

Tính giản lược

Công thức được biểu lộ cụ thể hơn tại giá trị thời hạn của tiền .

Trong các công thức dưới đây, i là lãi suất hiệu quả cho mỗi thời kỳ. FV và PV đại diện cho các giá trị tương lai và hiện tại của một khoản tiền. n đại diện cho số giai đoạn.

Đây là các công thức cơ bản nhất :

F V = P V ( 1 + i ) n { \ displaystyle FV = PV ( 1 + i ) ^ { n } \, } $FV=PV(1+i)^{n}\,$

Công thức trên tính toán giá trị tương lai (FV) của giá trị hiện tại của một đầu tư (PV) tích lũy với lãi suất cố định (i) cho n giai đoạn.

P V = F V ( 1 + i ) n { \ displaystyle PV = { \ frac { FV } { \ left ( 1 + i \ right ) ^ { n } } } \, } $PV={\frac {FV}{\left(1+i\right)^{n}}}\,$

Công thức trên tính toán giá trị hiện tại (PV) sẽ cần là bao nhiêu để tạo ra một giá trị nhất định trong tương lai (FV) nếu lãi suất (i) dồn tích cho n giai đoạn.

i = ( F V P V ) 1 n − 1 { \ displaystyle i = \ left ( { \ frac { FV } { PV } } \ right ) ^ { \ frac { 1 } { n } } – 1 } $i=\left({\frac {FV}{PV}}\right)^{\frac {1}{n}}-1$

Công thức trên tính toán lãi suất kép đạt được nếu đầu tư ban đầu PV cho ra giá trị của FV sau n giai đoạn dồn tích.

n = log ⁡ ( F V ) − log ⁡ ( P V ) log ⁡ ( 1 + i ) { \ displaystyle n = { \ frac { \ log ( FV ) – \ log ( PV ) } { \ log ( 1 + i ) } } } $n={\frac {\log(FV)-\log(PV)}{\log(1+i)}}$

Công thức trên tính toán số lượng thời kỳ cần thiết để có được FV từ PV đã cho và lãi suất (i). Hàm lô-ga-rít có thể ở bất kỳ cơ số nào, Thí dụ lô-ga-rít tự nhiên (ln), miễn là các cơ số phù hợp được dùng trong suốt tất cả các tính toán.

Công thức tính lãi kép hàng năm là

A = P ( 1 + r n ) n t { \ displaystyle A = P \ left ( 1 + { \ frac { r } { n } } \ right ) ^ { nt } } $A=P\left(1+{\frac {r}{n}}\right)^{nt}$

Ở đây ,

A = giá trị tương laiP = số tiền gốc (đầu tư ban đầu)r = lãi suất danh nghĩa hàng nămn = số lần tiền lãi được nhập gốc mỗi nămt = số năm tiền được mượn

Thí dụ dùng : Số tiền 1500.00 đô-la được gửi tại một nhà băng chi trả lãi suất vay hàng năm 4.3 %, được nhập gốc hàng quý. Tính số dư sau 6 năm .A. dùng công thức bên trên, với P = 1500, r = 0.043 ( 4.3 % ), n = 4, và t = 6 :

A = 1500 ( 1 + 0.043 4 ) 4 × 6 = 1938.84 { \ displaystyle A = 1500 \ left ( 1 + { \ frac { 0.043 } { 4 } } \ right ) ^ { 4 \ times 6 } = 1938.84 } $A=1500\left(1+{\frac {0.043}{4}}\right)^{4\times 6}=1938.84$

Như vậy, số dư sau 6 năm xê dịch 1,938. 84 đô-la. Lãi kép hoàn toàn có thể được tính bằng phương pháp trừ số tiền gốc khỏi số dư này .

Tính lãi kép định kỳ

Hàm số lượng cho lãi kép là một hàm mũ theo thời hạn .

A ( t ) =

(

1 +

r n

)

⌊ n t ⌋

{\displaystyle A(t)=A_{0}\left(1+{\frac {r}{n}}\right)^{\lfloor nt\rfloor }}

$A(t)=A_{0}\left(1+{\frac {r}{n}}\right)^{\lfloor nt\rfloor }$

t { \ displaystyle t } $t$ n { \ displaystyle n }n ⋅ t { \ displaystyle n \ cdot t } $n\cdot t$ r { \ displaystyle r } $r$ Lãi suất hàng năm danh nghĩa biểu diễn dưới dạng thập phân. chẳng hạn: 6% = 0.06⌊ n t ⌋ { \ displaystyle \ lfloor nt \ rfloor } $\lfloor nt\rfloor$ nt được làm tròn xuống giá trị nguyên gần nhất.

Khi n tăng lên, tỉ lệ này tiến tới giới hạn trên của er − 1. Tỉ lệ này được gọi là lãi kép liên tục, xem bên dưới.

Vì số tiền gốc A(0) chỉ đơn giản là một hệ số, nó thường được bỏ đi cho đơn giản, và hàm tích lũy kết quả được dùng trong lý thuyết tiền lãi thay thế. Các hàm tích lũy cho lãi đơn và lãi kép được liệt kê dưới đây:

a ( t ) = 1 + t r { \ displaystyle a ( t ) = 1 + tr \, } $a(t)=1+tr\,$ a ( t ) = ( 1 + r n ) n t { \ displaystyle a ( t ) = \ left ( 1 + { \ frac { r } { n } } \ right ) ^ { nt } } $a(t)=\left(1+{\frac {r}{n}}\right)^{nt}$

Lưu ý: A(t) là hàm số lượng và a(t) là hàm tích lũy.

Tính lãi kép liên tục

Tính lãi kép liên tục có thể được coi như việc làm cho kỳ tính lãi kép cực nhỏ; do đó đạt được bằng phương pháp lấy giới hạn của n tới vô cực. Người ta phải tham khảo ý kiến các định nghĩa của hàm số mũ cho chứng minh toán học của giới hạn này.

A ( t ) = A 0 e r t { \ displaystyle A ( t ) = A_ { 0 } e ^ { rt } } $A(t)=A_{0}e^{rt}$

A = P e r t { \ displaystyle A = Pe ^ { rt } } $A=Pe^{rt}$

Ảnh hưởng của tiền lãi

Trong toán học, các hàm tích lũy thường được biểu diễn trong các thuật ngữ của số e, cơ số của lô-ga-rít tự nhiên. Điều này tạo điều kiện cho việc dùng các phương pháp tính toán trong thao tác của công thức lãi vay.

Đối với một hàm tích lũy khả vi liên tục bất kỳ a(t) ảnh hưởng của tiền lãi, hoặc tổng quát hơn là Hoàn vốn kép lô-ga-rít hay hoàn vốn kép liên tục là một hàm theo thời gian được định nghĩa như sau:

a ′

( t )

a ( t )

{\displaystyle \delta _{t}={\frac {a`(t)}{a(t)}}\,}

$\delta _{t}={\frac {a`(t)}{a(t)}}\,$

nó là tỷ suất biến hóa theo thời hạn của lô-ga-rít tự nhiên của hàm tích góp .

Đảo lại:

a ( n ) =

∫

d t

{\displaystyle a(n)=e^{\int _{0}^{n}\delta _{t}\,dt}\,}

$a(n)=e^{\int _{0}^{n}\delta _{t}\,dt}\,$ (vì

a ( 0 ) = 1

{\displaystyle a(0)=1}

$a(0)=1$ )

Khi công thức bên trên được viết trong dạng phương trình vi phân, ảnh hưởng của tiền lãi đơn giản là hệ số của số lượng thay đổi:

d a ( t ) =

a ( t )

d t

{\displaystyle da(t)=\delta _{t}a(t)\,dt\,}

$da(t)=\delta _{t}a(t)\,dt\,$

Đối với lãi kép với lãi suất hàng năm không đổi r, ảnh hưởng của tiền lãi là một hằng số, và hàm tích lũy của lãi kép về khía cạnh ảnh hưởng của tiền lãi là lũy thừa đơn giản của số e:

δ = ln ⁡ ( 1 + r )

{\displaystyle \delta =\ln(1+r)\,}

$\delta =\ln(1+r)\,$ or

a ( t ) =

t δ

{\displaystyle a(t)=e^{t\delta }\,}

$a(t)=e^{t\delta }\,$

Ảnh hưởng của tiền lãi là ít hơn so với lãi suất vay thực hàng năm, nhưng nhiều hơn tỷ suất chiết khấu hiệu suất cao hàng năm. Nó là đối ứng của thời hạn e-folding. Xem thêm ký hiệu của lãi suất vay .

Một phương pháp mô hình hóa ảnh hưởng của lạm phát là với công thức của Stoodley:

= p +

1 + r s

s t

{\displaystyle \delta _{t}=p+{s \over {1+rse^{st}}}}

$\delta _{t}=p+{s \over {1+rse^{st}}}$ ở đây p, r và s được ước tính.

Cơ sở tính lãi kép

Để chuyển đổi một lãi suất từ một cơ sở lãi kép này sang một cơ sở lãi kép khác, công thức sau đây được áp dụng:

r 2 = [ ( 1 + r 1 n 1 ) n 1 n 2 − 1 ] n 2 { \ displaystyle r_ { 2 } = \ left [ \ left ( 1 + { \ frac { r_ { 1 } } { n_ { 1 } } } \ right ) ^ { \ frac { n_ { 1 } } { n_ { 2 } } } – 1 \ right ] n_ { 2 } } $r_{2}=\left[\left(1+{\frac {r_{1}}{n_{1}}}\right)^{\frac {n_{1}}{n_{2}}}-1\right]n_{2}$

ở đâyr1 là lãi suất quy định với tần suất tính lãi kép n1 vàr2 là lãi suất quy định với tần suất tính lãi kép n2.

Khi tiền lãi được tính lãi kép liên tục :

R = n ln ⁡ ( 1 + r / n ) { \ displaystyle R = n \ ln { \ left ( 1 + r / n \ right ) } } $R=n\ln {\left(1+r/n\right)}$

ở đâyR là lãi suất trên một cơ sở tính lãi kép liên tục vàr là lãi suất quy định với tần suất tính lãi kép n.

Trả tiền vay thế chấp ngân hàng hàng tháng

Tiền lãi cho vay thế chấp ngân hàng thường được tính lãi kép hàng tháng. Công thức cho các trả tiền hàng tháng được tìm thấy từ đối số sau đây .

I = Lãi suất trên giấy tờ (biểu diễn dạng thập phân, như 12% là 0.12)i = Lãi suất hàng tháng = I/12 (như vậy APR = (1+i)^12 – 1)T = Kỳ hạn vay theo số nămY= I•TX = ½ I•T = ½ Yn = 12•T = kỳ hạn theo thángL = Số tiền gốc của khoản vayP = tiền trả hàng tháng

Công thức đúng chuẩn cho P

Một công thức đúng mực cho trả tiền hàng tháng là

P = L i 1 − 1 ( 1 + i ) n { \ displaystyle P = { \ frac { Li } { 1 – { \ frac { 1 } { ( 1 + i ) ^ { n } } } } } } $P={\frac {Li}{1-{\frac {1}{(1+i)^{n}}}}}$

hoặc tương tự

P = L i 1 − e − n ln ⁡ ( 1 + i ) { \ displaystyle P = { \ frac { Li } { 1 – e ^ { – n \ ln ( 1 + i ) } } } } $P={\frac {Li}{1-e^{-n\ln(1+i)}}}$

Điều này có thể được bắt nguồn bằng phương pháp xem xét bao nhiêu tiền đã được trả để lại được thanh toán sau mỗi tháng. Sau tháng đầu tiên

= ( 1 + i ) L − P

{\displaystyle L_{1}=(1+i)L-P}

$L_{1}=(1+i)L-P$ is left, i.e. số tiền ban đầu đã gia tăng việc bớt trả tiền. Nếu toàn bộ khoản vay được tái trả tiền sau 1 tháng thì

= 0

{\displaystyle L_{1}=0}

$L_{1}=0$ nên

L =

1 + i

{\displaystyle L={\frac {P}{1+i}}}

$L={\frac {P}{1+i}}$ Sau tháng thứ hai

= ( 1 + i )

− P

{\displaystyle L_{2}=(1+i)L_{1}-P}

$L_{2}=(1+i)L_{1}-P$ is left, that is

= ( 1 + i ) ( ( 1 + i ) L − P ) − P

{\displaystyle L_{2}=(1+i)((1+i)L-P)-P}

$L_{2}=(1+i)((1+i)L-P)-P$ . Nếu toàn bộ khoản vay được repaid sau 2 tháng

= 0

{\displaystyle L_{2}=0}

$L_{2}=0$ this gives phương trình

L =

1 + i

( 1 + i

)

{\displaystyle L={\frac {P}{1+i}}+{\frac {P}{(1+i)^{2}}}}

$L={\frac {P}{1+i}}+{\frac {P}{(1+i)^{2}}}$ . Phương trình này generalises cho một kỳ hạn n tháng,

L = P

∑

j = 1

( 1 + i

)

{\displaystyle L=P\sum _{j=1}^{n}{\frac {1}{(1+i)^{j}}}}

$L=P\sum _{j=1}^{n}{\frac {1}{(1+i)^{j}}}$ . Đây là tổng dãy số lũy thừa, và cụ thể trong toán học là một chuỗi hình học (geometric series) hoặc một cấp số nhân (arithmetic sequence) có tổng

L = P i ( 1 − 1 ( 1 + i ) n ) { \ displaystyle L = { \ frac { P } { i } } \ left ( 1 – { \ frac { 1 } { ( 1 + i ) ^ { n } } } \ right ) } $L={\frac {P}{i}}\left(1-{\frac {1}{(1+i)^{n}}}\right)$

which can be rearranged to give

P = L i 1 − 1 ( 1 + i ) n = L i 1 − e − n ln ⁡ ( 1 + i ) { \ displaystyle P = { \ frac { Li } { 1 – { \ frac { 1 } { ( 1 + i ) ^ { n } } } } } = { \ frac { Li } { 1 – e ^ { – n \ ln ( 1 + i ) } } } } $P={\frac {Li}{1-{\frac {1}{(1+i)^{n}}}}}={\frac {Li}{1-e^{-n\ln(1+i)}}}$

Công thức này cho việc trả tiền hàng tháng trong vay thế chấp ngân hàng tại Hoa Kỳ là đúng mực và là cái mà các ngân hàng nhà nước dùng .

Công thức gần đúng cho P

Một công thức mà là chính xác để trong một vài phần trăm có thể được tìm thấy bằng phương pháp lưu ý rằng đối với các lãi suất giấy tờ Hoa Kỳ điển hình (

I $I<8\%$ và kỳ hạn T=10–30 năm), lãi suất giấy tờ hàng tháng là nhỏ so với 1:

i ≪ 1

{\displaystyle i\ll 1}

$i\ll 1$ để

ln ⁡ ( 1 + i ) ≈ i

{\displaystyle \ln(1+i)\approx i}

$\ln(1+i)\approx i$ tạo ra đơn giản hóa đối với

P ≈

L i

1 −

− n i

L n

n i

1 −

− n i

{\displaystyle P\approx {\frac {Li}{1-e^{-ni}}}={\frac {L}{n}}{\frac {ni}{1-e^{-ni}}}}

$P\approx {\frac {Li}{1-e^{-ni}}}={\frac {L}{n}}{\frac {ni}{1-e^{-ni}}}$

điều này cho thấy định nghĩa các biến phụ trợ

Y ≡ n i = T I

{\displaystyle Y\equiv ni=TI}

$Y\equiv ni=TI$

≡

L n

{\displaystyle P_{0}\equiv {\frac {L}{n}}}

$P_{0}\equiv {\frac {L}{n}}$ .

{\displaystyle P_{0}}

$P_{0}$ là trả tiền hàng tháng được yêu cầu đối với trả hết khoản vay lãi vay bằng không trong

{\displaystyle n}

trả góp. Trong các điều kiện của các biến này xấp xỉ này có thể được viết

P ≈

1 −

− Y

{\displaystyle P\approx P_{0}{\frac {Y}{1-e^{-Y}}}}

$P\approx P_{0}{\frac {Y}{1-e^{-Y}}}$

Hàm

f ( Y ) ≡

1 −

− Y

−

Y 3

{\displaystyle f(Y)\equiv {\frac {Y}{1-e^{-Y}}}-{\frac {Y}{3}}}

$f(Y)\equiv {\frac {Y}{1-e^{-Y}}}-{\frac {Y}{3}}$ thậm chí còn:

f ( Y ) = f ( − Y )

{\displaystyle f(Y)=f(-Y)}

$f(Y)=f(-Y)$ ngụ ý rằng nó có thể được mở rộng ngay cả trong các lũy thừa của

{\displaystyle Y}

Nó ngay lập tức sau đó

1 −

− Y

{\displaystyle {\frac {Y}{1-e^{-Y}}}}

${\frac {Y}{1-e^{-Y}}}$ có thể được mở rộng ngay cả trong các lũy thừa của

{\displaystyle Y}

cộng kỳ hạn đơn:

{\displaystyle Y/2}

$Y/2$

Nó sẽ chứng tỏ thuận tiện sau đó để xác lập

X =

1 2

Y =

1 2

I T

{\displaystyle X={\frac {1}{2}}Y={\frac {1}{2}}IT}

$X={\frac {1}{2}}Y={\frac {1}{2}}IT$

so that

P ≈

2 X

1 −

− 2 X

{\displaystyle P\approx P_{0}{\frac {2X}{1-e^{-2X}}}}

$P\approx P_{0}{\frac {2X}{1-e^{-2X}}}$ which can be expanded:

P ≈

(

1 + X +

−

1 45

+ …

)

{\displaystyle P\approx P_{0}\left(1+X+{\frac {X^{2}}{3}}-{\frac {1}{45}}X^{4}+\dots \right)}

$P\approx P_{0}\left(1+X+{\frac {X^{2}}{3}}-{\frac {1}{45}}X^{4}+\dots \right)$

khi ellipses cho thấy các điều mà là số mũ cao hơn thậm chí các lũy thừa của

{\displaystyle X}

. Biểu thức

P ≈

(

1 + X +

)

{\displaystyle P\approx P_{0}\left(1+X+{\frac {X^{2}}{3}}\right)}

$P\approx P_{0}\left(1+X+{\frac {X^{2}}{3}}\right)$

là hợp lệ để tốt hơn 1% được cung cấp

X ≤ 1

{\displaystyle X\leq 1}

$X\leq 1$ .

Cho một khoản vay thế chấp ngân hàng với kỳ hạn 30 năm và với lãi suất vay sách vở 4.5 % tất cả chúng ta tìm được :

T = 30

{\displaystyle T=30}

$T=30$

I = .045

{\displaystyle I=.045}

$I=.045$

X =

1 2

I T =

1 2

× .045 × 30 = .675

{\displaystyle X={\frac {1}{2}}IT={\frac {1}{2}}\times .045\times 30=.675}

$X={\frac {1}{2}}IT={\frac {1}{2}}\times .045\times 30=.675$

cho thấy rằng xê dịch

P ≈

(

1 + X +

1 3

)

{\displaystyle P\approx P_{0}\left(1+X+{\frac {1}{3}}X^{2}\right)}

$P\approx P_{0}\left(1+X+{\frac {1}{3}}X^{2}\right)$ là chính xác hơn một phần trăm đối với các điều kiện thế chấp điển hình của Mỹ vào tháng 1 năm 2009. Công thức trở nên kém chính xác hơn đối với các lãi suất cao hơn và kỳ hạn dài hơn.

Cho một kỳ hạn vay 30 năm trên một khoản vay 120.000 đô-la và lãi suất vay sách vở 4.5 % tất cả chúng ta tìm được :

L = 120000

{\displaystyle L=120000}

$L=120000$

$ 120 , 000

360

= $ 333.33

{\displaystyle P_{0}={\frac {\$120,000}{360}}=\$333.33}

$P_{0}={\frac {\$120,000}{360}}=\$333.33$

so that

P ≈

(

1 + X +

1 3

)

= $ 333.33 ( 1 + .675 +

.675

3 ) = $ 608.96

{\displaystyle P\approx P_{0}\left(1+X+{\frac {1}{3}}X^{2}\right)=\$333.33(1+.675+.675^{2}/3)=\$608.96}

$P\approx P_{0}\left(1+X+{\frac {1}{3}}X^{2}\right)=\$333.33(1+.675+.675^{2}/3)=\$608.96$

Số tiền thanh toán chính xác là

P = $ 608.02

{\displaystyle P=\$608.02}

$P=\$608.02$ nên xấp xỉ này là giản ước quá mức khoảng 6%.

Tính lãi kép đã từng bị coi là loại cho vay nặng lãi tồi tệ nhất, và đã bị phán quyết nặng nề bởi pháp luật La Mã, cũng như thông luật của nhiều nước khác. Trong một đoạn văn, Thánh Kinh chỉ ra việc tính tiền lãi theo phương pháp sau đây :

“ Đừng lấy lãi nặng hoặc lãi vay từ anh ta ; nhưng kính sợ Thiên Chúa của bạn, rằng anh trai của bạn hoàn toàn có thể sống với bạn. Bạn sẽ không cho anh ta vay tiền của bạn với lãi nặng, và cũng không anh ta vay thức ăn của bạn để có doanh thu. ”Leviticus 25:36-37

Qur’an đề cập một phương pháp rõ ràng đến lãi kép như một tội lớn. Cho vay nặng lãi ( lãi suất vay áp bức ), được biết đến trong tiếng Ả Rập là ” riba “, được coi là sai :

“ Hỡi những người tin ! Nuốt không cho vay nặng lãi, tăng gấp đôi và gấp bốn lần ( số tiền cho vay ). Thực hiện trách nhiệm của mình với Allah, để đồng đội hoàn toàn có thể thành công xuất sắc. ”Qur’an 3:130

Cuốn sách của Richard Witt các câu hỏi số học, xuất bản năm 1613, là một bước ngoặt trong lịch sử của lãi kép. Nó đã được hoàn toàn dành cho đối tượng (trước đây gọi là anatocism), trong khi các nhà văn trước đó đã thường chỉ dành cho lãi kép chỉ trong một chương ngắn trong các sách giáo khoa toán học. Cuốn sách Witt đưa các bảng dựa trên 10% (lãi suất tối đa cho các khoản vay được phép) và các lãi suất khác cho các mục đích khác nhau, chẳng hạn như xác định giá trị hợp đồng thuê tài sản. Witt là một học giả toán học London và cuốn sách của ông là đáng chú ý cho rõ ràng của nó thể hiện, chiều sâu của cái nhìn sâu sắc và chính xác của tính toán, với 124 Thí dụ đã làm việc.

^Department of Justice. The Interest Act specifies that interest is not recoverable unless the mortgage loan contains a statement showing the rate of interest chargeable, “calculated yearly or half-yearly, not in advance.” In practice, banks use the half-yearly rate.http://laws.justice.gc.ca/en/showdoc/cs/I-15/bo-ga:s_6//en#anchorbo-ga:s_6 Interest Act (Canada),. The Interest Act specifies that interest is not recoverable unless the mortgage loan contains a statement showing the rate of interest chargeable, “calculated yearly or half-yearly, not in advance.” In practice, banks use the half-yearly rate.^ Bài này kết hợp văn bản từ ấn bản hiện nay thuộc Chambers, Ephraim biên tập (1728). Cyclopædia, và or an Universal Dictionary of Arts and Sciences (ấn bản 1). James & John Knapton, et al. Bài này phối hợp văn bản từ ấn bản lúc bấy giờ thuộc khoanh vùng phạm vi công cộng^

Lewin, C G (1970). “An Early Book on Compound Interest – Richard Witt’s Arithmeticall Questions”. Journal of the Institute of Actuaries. 96 (1): 121–132.

Xem thêm: KOL (marketing) – Wikipedia tiếng Việt

Lewin, C G (1981). “Compound Interest in the Seventeenth Century”. Journal of the Institute of Actuaries. 108 (3): 423–442.