Phần nguyên là gì – Wikipedia tiếng Việt

0 Shares

Các hàm Floor và ceiling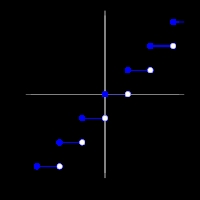Hàm Floor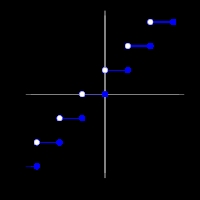Hàm Ceiling

Trong toán học và khoa học máy tính, hàm floor và ceiling là các quy tắc cho tương ứng một vài thực vào một vài nguyên gần nhất bên trái và bên phải số đã cho. Vậy floor(x) là số nguyên lớn nhất không vượt quá x, còn ceiling(x) là số nguyên nhỏ nhất không nhỏ hơn x.

Phần nguyên là gì – Wikipedia tiếng Việt

Gauss giới thiệu cặp ngoặc vuông [x] cho hàm floor trong tương hỗ bậc hai (1808). Nó vẫn là ký hiệu tiêu chuẩn trong toán học cho đến khi Iverson giới thiệu các hàm “floor” và “ceiling” với các ký hiệu

Bạn đang đọc: Phần nguyên là gì – Wikipedia tiếng Việt

⌊ x ⌋

{\displaystyle \lfloor x\rfloor }

$\lfloor x\rfloor$ và

⌈ x ⌉

{\displaystyle \lceil x\rceil }

$\lceil x\rceil$ vào năm 1962 trong ngôn ngữ lập trình APL của ông ấy. Bây giờ cả hai cách ký hiệu vẫn đang được sử dụng trong toán học.

Floor(x) ⌊ ⌋ { \ displaystyle \ lfloor \ ; \ rfloor } $\lfloor \;\rfloor$ Ceiling(x) ⌈ ⌉ { \ displaystyle \ lceil \ ; \ rceil } $\lceil \;\rceil$ Phần lẻ { } { \ displaystyle \ { \ ; \ } } $\{\;\}$

−2.7

−3

−2

0.3

−2

12/5 = 2.4

2/5 = 0.4

2.7

0.7

Đọc phần bên dưới để biết thêm về định nghĩa phần lẻ .

Định nghĩa và đặc thù

Trong các công thức dưới đây x và y là các số thực, k, m, và n là các số nguyên, và

{\displaystyle \mathbb {Z} }

$\mathbb {Z}$ là tập hợp số nguyên (số dương, số âm, và không).

Floor và ceiling hoàn toàn có thể được định nghĩa bằng tập hợp như sau

⌊ x ⌋ = max { n ∈ Z ∣ n ≤ x }, { \ displaystyle \ lfloor x \ rfloor = \ max \, \ { n \ in \ mathbb { Z } \ mid n \ leq x \ }, } $\lfloor x\rfloor =\max \,\{n\in \mathbb {Z} \mid n\leq x\},$ ⌈ x ⌉ = min { n ∈ Z ∣ n ≥ x }. { \ displaystyle \ lceil x \ rceil = \ min \, \ { n \ in \ mathbb { Z } \ mid n \ geq x \ }. } $\lceil x\rceil =\min \,\{n\in \mathbb {Z} \mid n\geq x\}.$

Trong nửa khoảng có độ dài bằng một có duy nhất một vài nguyên, vậy với số thực x tùy ý, có duy nhất cặp m, n thỏa mãn:

x − 1 $x-1<m\leq x\leq n<x+1.\;$

Khi đó

⌊ x ⌋ = m

{\displaystyle \lfloor x\rfloor =m\;}

$\lfloor x\rfloor =m\;$ và

⌈ x ⌉ = n

{\displaystyle \;\lceil x\rceil =n\;}

$\;\lceil x\rceil =n\;$ có thể là định nghĩa cho các hàm floor và ceiling.

Phần lẻ x ký hiệu

{ x }

{\displaystyle \{x\}}

$\{x\}$ là hàm số định nghĩa theo công thức sau,

{ x } = x − ⌊ x ⌋ ,

{\displaystyle \{x\}=x-\lfloor x\rfloor ,}

$\{x\}=x-\lfloor x\rfloor ,$ và toán tử mô-đun được định nghĩa theo công thức:

mod

y = x − y

⌊

x y

⌋

{\displaystyle x\,{\bmod {\,}}y=x-y\left\lfloor {\frac {x}{y}}\right\rfloor .}

$x\,{\bmod {\,}}y=x-y\left\lfloor {\frac {x}{y}}\right\rfloor .$

Các công thức dưới đây sử dụng để rút gọn các biểu thức chứa các hàm floor, ceiling. [ 5 ]

⌊ x ⌋ = n

⇔

≤ x ${\begin{aligned}\lfloor x\rfloor =n&\;\;\Leftrightarrow &n&\leq x<n+1,\\\lceil x\rceil =n&\;\;\Leftrightarrow &n-1&<x\leq n,\\\lfloor x\rfloor =n&\;\;\Leftrightarrow &x-1&<n\leq x,\\\lceil x\rceil =n&\;\;\Leftrightarrow &x&\leq n<x+1.\end{aligned}}$

In the language of order theory, the floor function is a residuated mapping, that is, part of a Galois connection : it is the upper adjoint of the function that embeds the integers into the reals .

x ${\begin{aligned}x<n&\;\;\Leftrightarrow &\lfloor x\rfloor &<n,\\n<x&\;\;\Leftrightarrow &n&<\lceil x\rceil ,\\x\leq n&\;\;\Leftrightarrow &\lceil x\rceil &\leq n,\\n\leq x&\;\;\Leftrightarrow &n&\leq \lfloor x\rfloor .\end{aligned}}$

Các công thức dưới đây đưa ra quy tắc khi cộng thêm 1 số ít nguyên vào các hàm phần nguyên như thế nào :

⌊ x + n ⌋ = ⌊ x ⌋ + n, ⌈ x + n ⌉ = ⌈ x ⌉ + n, { x + n } = { x }. { \ displaystyle { \ begin { aligned } \ lfloor x + n \ rfloor và = \ lfloor x \ rfloor + n, \ \ \ lceil x + n \ rceil và = \ lceil x \ rceil + n, \ \ \ { x + n \ } và = \ { x \ }. \ end { aligned } } } ${\begin{aligned}\lfloor x+n\rfloor &=\lfloor x\rfloor +n,\\\lceil x+n\rceil &=\lceil x\rceil +n,\\\{x+n\}&=\{x\}.\end{aligned}}$

Các công thức trên không đúng nếu n không phải số nguyên, tuy vậy :

⌊ x ⌋ + ⌊ y ⌋ ≤ ⌊ x + y ⌋ ≤ ⌊ x ⌋ + ⌊ y ⌋ + 1, ⌈ x ⌉ + ⌈ y ⌉ − 1 ≤ ⌈ x + y ⌉ ≤ ⌈ x ⌉ + ⌈ y ⌉. { \ displaystyle { \ begin { aligned } và \ lfloor x \ rfloor + \ lfloor y \ rfloor và \ leq \ ; \ lfloor x + y \ rfloor \ ; và \ leq \ ; \ lfloor x \ rfloor + \ lfloor y \ rfloor + 1, \ \ và \ lceil x \ rceil + \ lceil y \ rceil – 1 và \ leq \ ; \ lceil x + y \ rceil \ ; và \ leq \ ; \ lceil x \ rceil + \ lceil y \ rceil. \ end { aligned } } } ${\begin{aligned}&\lfloor x\rfloor +\lfloor y\rfloor &\leq \;\lfloor x+y\rfloor \;&\leq \;\lfloor x\rfloor +\lfloor y\rfloor +1,\\&\lceil x\rceil +\lceil y\rceil -1&\leq \;\lceil x+y\rceil \;&\leq \;\lceil x\rceil +\lceil y\rceil .\end{aligned}}$

Mối liên hệ giữa các hàm

Từ định nghĩa thuận tiện có được

⌊ x ⌋ ≤ ⌈ x ⌉, { \ displaystyle \ lfloor x \ rfloor \ leq \ lceil x \ rceil, } $\lfloor x\rfloor \leq \lceil x\rceil ,$ x là số nguyên, i.e.⌈ x ⌉ − ⌊ x ⌋ = { 0 if x ∈ Z 1 if x ∉ Z { \ displaystyle \ lceil x \ rceil – \ lfloor x \ rfloor = { \ begin { cases } 0 và { \ mbox { if } } x \ in \ mathbb { Z } \ \ 1 và { \ mbox { if } } x \ not \ in \ mathbb { Z } \ end { cases } } } $\lceil x\rceil -\lfloor x\rfloor ={\begin{cases}0&{\mbox{ if }}x\in \mathbb {Z} \\1&{\mbox{ if }}x\not \in \mathbb {Z} \end{cases}}$

n là số nguyên thì :

⌊ n ⌋ = ⌈ n ⌉ = n. { \ displaystyle \ lfloor n \ rfloor = \ lceil n \ rceil = n. } $\lfloor n\rfloor =\lceil n\rceil =n.$

Khi số âm là đối số thì đổi các hàm floor và ceil đồng thời đưa dấu trừ ra ngoài :

⌊ x ⌋ + ⌈ − x ⌉ = 0, { \ displaystyle \ lfloor x \ rfloor + \ lceil – x \ rceil = 0, } $\lfloor x\rfloor +\lceil -x\rceil =0,$ ⌊ − x ⌋ = − ⌈ x ⌉, { \ displaystyle \ lfloor – x \ rfloor = – \ lceil x \ rceil, } $\lfloor -x\rfloor =-\lceil x\rceil ,$ ⌈ − x ⌉ = − ⌊ x ⌋, { \ displaystyle \ lceil – x \ rceil = – \ lfloor x \ rfloor, } $\lceil -x\rceil =-\lfloor x\rfloor ,$

⌊ x ⌋ + ⌊ − x ⌋ = { 0 if x ∈ Z − 1 if x ∉ Z, { \ displaystyle \ lfloor x \ rfloor + \ lfloor – x \ rfloor = { \ begin { cases } 0 và { \ mbox { if } } x \ in \ mathbb { Z } \ \ – 1 và { \ mbox { if } } x \ not \ in \ mathbb { Z }, \ end { cases } } } $\lfloor x\rfloor +\lfloor -x\rfloor ={\begin{cases}0&{\mbox{ if }}x\in \mathbb {Z} \\-1&{\mbox{ if }}x\not \in \mathbb {Z} ,\end{cases}}$

⌈ x ⌉ + ⌈ − x ⌉ = { 0 if x ∈ Z 1 if x ∉ Z. { \ displaystyle \ lceil x \ rceil + \ lceil – x \ rceil = { \ begin { cases } 0 và { \ mbox { if } } x \ in \ mathbb { Z } \ \ 1 và { \ mbox { if } } x \ not \ in \ mathbb { Z }. \ end { cases } } } $\lceil x\rceil +\lceil -x\rceil ={\begin{cases}0&{\mbox{ if }}x\in \mathbb {Z} \\1&{\mbox{ if }}x\not \in \mathbb {Z} .\end{cases}}$

Về phần lẻ :

{ x } + { − x } = { 0 if x ∈ Z 1 if x ∉ Z. { \ displaystyle \ { x \ } + \ { – x \ } = { \ begin { cases } 0 và { \ mbox { if } } x \ in \ mathbb { Z } \ \ 1 và { \ mbox { if } } x \ not \ in \ mathbb { Z }. \ end { cases } } } $\{x\}+\{-x\}={\begin{cases}0&{\mbox{ if }}x\in \mathbb {Z} \\1&{\mbox{ if }}x\not \in \mathbb {Z} .\end{cases}}$

Floor, ceiling, và phần lẻ là hàm idempotent :

⌊ ⌊ x ⌋ ⌋ = ⌊ x ⌋, ⌈ ⌈ x ⌉ ⌉ = ⌈ x ⌉, { { x } } = { x }. { \ displaystyle { \ begin { aligned } { \ Big \ lfloor } \ lfloor x \ rfloor { \ Big \ rfloor } và = \ lfloor x \ rfloor, \ \ { \ Big \ lceil } \ lceil x \ rceil { \ Big \ rceil } và = \ lceil x \ rceil, \ \ { \ Big \ { } \ { x \ } { \ Big \ } } và = \ { x \ }. \ \ \ end { aligned } } } ${\begin{aligned}{\Big \lfloor }\lfloor x\rfloor {\Big \rfloor }&=\lfloor x\rfloor ,\\{\Big \lceil }\lceil x\rceil {\Big \rceil }&=\lceil x\rceil ,\\{\Big \{}\{x\}{\Big \}}&=\{x\}.\\\end{aligned}}$

Dễ thấy các đẳng thức sau là đúng :

⌊ ⌈ x ⌉ ⌋ = ⌈ x ⌉, ⌈ ⌊ x ⌋ ⌉ = ⌊ x ⌋. { \ displaystyle { \ begin { aligned } { \ Big \ lfloor } \ lceil x \ rceil { \ Big \ rfloor } và = \ lceil x \ rceil, \ \ { \ Big \ lceil } \ lfloor x \ rfloor { \ Big \ rceil } và = \ lfloor x \ rfloor. \ \ \ end { aligned } } } ${\begin{aligned}{\Big \lfloor }\lceil x\rceil {\Big \rfloor }&=\lceil x\rceil ,\\{\Big \lceil }\lfloor x\rfloor {\Big \rceil }&=\lfloor x\rfloor .\\\end{aligned}}$

Với y có định thì, x mod y là hàm idempotent:

( x mod y ) mod y = x mod y. { \ displaystyle ( x \, { \ bmod { \, } } y ) \, { \ bmod { \, } } y = x \, { \ bmod { \, } } y. \ ; } $(x\,{\bmod {\,}}y)\,{\bmod {\,}}y=x\,{\bmod {\,}}y.\;$

Cũng từ định nghĩa ta có ,

{ x } = x mod 1. { \ displaystyle \ { x \ } = x \, { \ bmod { \, } } 1. \ ; } $\{x\}=x\,{\bmod {\,}}1.\;$

Nếu n ≠ 0,

0 ≤ { m n } ≤ 1 − 1 | n |. { \ displaystyle 0 \ leq \ left \ { { \ frac { m } { n } } \ right \ } \ leq 1 – { \ frac { 1 } { | n | } }. } $0\leq \left\{{\frac {m}{n}}\right\}\leq 1-{\frac {1}{|n|}}.$

Nếu n > 0,

⌊ x + m n ⌋ = ⌊ ⌊ x ⌋ + m n ⌋, { \ displaystyle \ left \ lfloor { \ frac { x + m } { n } } \ right \ rfloor = \ left \ lfloor { \ frac { \ lfloor x \ rfloor + m } { n } } \ right \ rfloor, } $\left\lfloor {\frac {x+m}{n}}\right\rfloor =\left\lfloor {\frac {\lfloor x\rfloor +m}{n}}\right\rfloor ,$ ⌈ x + m n ⌉ = ⌈ ⌈ x ⌉ + m n ⌉. { \ displaystyle \ left \ lceil { \ frac { x + m } { n } } \ right \ rceil = \ left \ lceil { \ frac { \ lceil x \ rceil + m } { n } } \ right \ rceil. } $\left\lceil {\frac {x+m}{n}}\right\rceil =\left\lceil {\frac {\lceil x\rceil +m}{n}}\right\rceil .$

Nếu m > 0,

n = ⌈ n m ⌉ + ⌈ n − 1 m ⌉ + ⋯ + ⌈ n − m + 1 m ⌉, { \ displaystyle n = \ left \ lceil { \ frac { n } { m } } \ right \ rceil + \ left \ lceil { \ frac { n-1 } { m } } \ right \ rceil + \ dots + \ left \ lceil { \ frac { n-m+1 } { m } } \ right \ rceil, } $n=\left\lceil {\frac {n}{m}}\right\rceil +\left\lceil {\frac {n-1}{m}}\right\rceil +\dots +\left\lceil {\frac {n-m+1}{m}}\right\rceil ,$ n = ⌊ n m ⌋ + ⌊ n + 1 m ⌋ + ⋯ + ⌊ n + m − 1 m ⌋. { \ displaystyle n = \ left \ lfloor { \ frac { n } { m } } \ right \ rfloor + \ left \ lfloor { \ frac { n + 1 } { m } } \ right \ rfloor + \ dots + \ left \ lfloor { \ frac { n + m-1 } { m } } \ right \ rfloor. } $n=\left\lfloor {\frac {n}{m}}\right\rfloor +\left\lfloor {\frac {n+1}{m}}\right\rfloor +\dots +\left\lfloor {\frac {n+m-1}{m}}\right\rfloor .$

Với m = 2:

n = ⌊ n 2 ⌋ + ⌈ n 2 ⌉. { \ displaystyle n = \ left \ lfloor { \ frac { n } { 2 } } \ right \ rfloor + \ left \ lceil { \ frac { n } { 2 } } \ right \ rceil. } $n=\left\lfloor {\frac {n}{2}}\right\rfloor +\left\lceil {\frac {n}{2}}\right\rceil .$

Tổng quát, với m > 0,

⌈ m x ⌉ = ⌈ x ⌉ + ⌈ x − 1 m ⌉ + ⋯ + ⌈ x − m − 1 m ⌉, { \ displaystyle \ lceil mx \ rceil = \ left \ lceil x \ right \ rceil + \ left \ lceil x – { \ frac { 1 } { m } } \ right \ rceil + \ dots + \ left \ lceil x – { \ frac { m-1 } { m } } \ right \ rceil, } $\lceil mx\rceil =\left\lceil x\right\rceil +\left\lceil x-{\frac {1}{m}}\right\rceil +\dots +\left\lceil x-{\frac {m-1}{m}}\right\rceil ,$ ⌊ m x ⌋ = ⌊ x ⌋ + ⌊ x + 1 m ⌋ + ⋯ + ⌊ x + m − 1 m ⌋. { \ displaystyle \ lfloor mx \ rfloor = \ left \ lfloor x \ right \ rfloor + \ left \ lfloor x + { \ frac { 1 } { m } } \ right \ rfloor + \ dots + \ left \ lfloor x + { \ frac { m-1 } { m } } \ right \ rfloor. } $\lfloor mx\rfloor =\left\lfloor x\right\rfloor +\left\lfloor x+{\frac {1}{m}}\right\rfloor +\dots +\left\lfloor x+{\frac {m-1}{m}}\right\rfloor .$

Biểu thức dưới đây sử dụng để chuyển đổi floor sang ceiling và ngược lại (m > 0)

⌈ n m ⌉ = ⌊ n + m − 1 m ⌋ = ⌊ n − 1 m ⌋ + 1, { \ displaystyle \ left \ lceil { \ frac { n } { m } } \ right \ rceil = \ left \ lfloor { \ frac { n + m-1 } { m } } \ right \ rfloor = \ left \ lfloor { \ frac { n-1 } { m } } \ right \ rfloor + 1, } $\left\lceil {\frac {n}{m}}\right\rceil =\left\lfloor {\frac {n+m-1}{m}}\right\rfloor =\left\lfloor {\frac {n-1}{m}}\right\rfloor +1,$ ⌊ n m ⌋ = ⌈ n − m + 1 m ⌉ = ⌈ n + 1 m ⌉ − 1, { \ displaystyle \ left \ lfloor { \ frac { n } { m } } \ right \ rfloor = \ left \ lceil { \ frac { n-m+1 } { m } } \ right \ rceil = \ left \ lceil { \ frac { n + 1 } { m } } \ right \ rceil – 1, } $\left\lfloor {\frac {n}{m}}\right\rfloor =\left\lceil {\frac {n-m+1}{m}}\right\rceil =\left\lceil {\frac {n+1}{m}}\right\rceil -1,$

Nếu m và n là các số nguyên dương và nguyên tố cùng nhau, thì

∑ i = 1 n − 1 ⌊ i m n ⌋ = 1 2 ( m − 1 ) ( n − 1 ). { \ displaystyle \ sum _ { i = 1 } ^ { n-1 } \ left \ lfloor { \ frac { im } { n } } \ right \ rfloor = { \ frac { 1 } { 2 } } ( m-1 ) ( n-1 ). } $\sum _{i=1}^{n-1}\left\lfloor {\frac {im}{n}}\right\rfloor ={\frac {1}{2}}(m-1)(n-1).$

Vì vế phải của biểu thức trên đối xứng theo m và n, vậy nên ta có biểu thức dưới đây

⌊ m n ⌋ + ⌊ 2 m n ⌋ + ⋯ + ⌊ ( n − 1 ) m n ⌋ = ⌊ n m ⌋ + ⌊ 2 n m ⌋ + ⋯ + ⌊ ( m − 1 ) n m ⌋. { \ displaystyle \ left \ lfloor { \ frac { m } { n } } \ right \ rfloor + \ left \ lfloor { \ frac { 2 m } { n } } \ right \ rfloor + \ dots + \ left \ lfloor { \ frac { ( n-1 ) m } { n } } \ right \ rfloor = \ left \ lfloor { \ frac { n } { m } } \ right \ rfloor + \ left \ lfloor { \ frac { 2 n } { m } } \ right \ rfloor + \ dots + \ left \ lfloor { \ frac { ( m-1 ) n } { m } } \ right \ rfloor. } $\left\lfloor {\frac {m}{n}}\right\rfloor +\left\lfloor {\frac {2m}{n}}\right\rfloor +\dots +\left\lfloor {\frac {(n-1)m}{n}}\right\rfloor =\left\lfloor {\frac {n}{m}}\right\rfloor +\left\lfloor {\frac {2n}{m}}\right\rfloor +\dots +\left\lfloor {\frac {(m-1)n}{m}}\right\rfloor .$

Tổng quát, nếu m và n nguyên dương:

⌊ x n ⌋ + ⌊ m + x n ⌋ + ⌊ 2 m + x n ⌋ + ⋯ + ⌊ ( n − 1 ) m + x n ⌋ = ⌊ x m ⌋ + ⌊ n + x m ⌋ + ⌊ 2 n + x m ⌋ + ⋯ + ⌊ ( m − 1 ) n + x m ⌋. { \ displaystyle { \ begin { aligned } và \ left \ lfloor { \ frac { x } { n } } \ right \ rfloor + \ left \ lfloor { \ frac { m + x } { n } } \ right \ rfloor + \ left \ lfloor { \ frac { 2 m + x } { n } } \ right \ rfloor + \ dots + \ left \ lfloor { \ frac { ( n-1 ) m + x } { n } } \ right \ rfloor \ \ = và \ left \ lfloor { \ frac { x } { m } } \ right \ rfloor + \ left \ lfloor { \ frac { n + x } { m } } \ right \ rfloor + \ left \ lfloor { \ frac { 2 n + x } { m } } \ right \ rfloor + \ dots + \ left \ lfloor { \ frac { ( m-1 ) n + x } { m } } \ right \ rfloor. \ end { aligned } } } ${\begin{aligned}&\left\lfloor {\frac {x}{n}}\right\rfloor +\left\lfloor {\frac {m+x}{n}}\right\rfloor +\left\lfloor {\frac {2m+x}{n}}\right\rfloor +\dots +\left\lfloor {\frac {(n-1)m+x}{n}}\right\rfloor \\=&\left\lfloor {\frac {x}{m}}\right\rfloor +\left\lfloor {\frac {n+x}{m}}\right\rfloor +\left\lfloor {\frac {2n+x}{m}}\right\rfloor +\dots +\left\lfloor {\frac {(m-1)n+x}{m}}\right\rfloor .\end{aligned}}$

Cho các số nguyên dương m, n và số thực ngẫu nhiên x:

⌊ ⌊ x / m ⌋ n ⌋ = ⌊ x m n ⌋ { \ displaystyle \ left \ lfloor { \ frac { \ lfloor x / m \ rfloor } { n } } \ right \ rfloor = \ left \ lfloor { \ frac { x } { mn } } \ right \ rfloor } $\left\lfloor {\frac {\lfloor x/m\rfloor }{n}}\right\rfloor =\left\lfloor {\frac {x}{mn}}\right\rfloor$ ⌈ ⌈ x / m ⌉ n ⌉ = ⌈ x m n ⌉ { \ displaystyle \ left \ lceil { \ frac { \ lceil x / m \ rceil } { n } } \ right \ rceil = \ left \ lceil { \ frac { x } { mn } } \ right \ rceil } $\left\lceil {\frac {\lceil x/m\rceil }{n}}\right\rceil =\left\lceil {\frac {x}{mn}}\right\rceil$

Sự liên tục

Không có hàm nào chúng ta đang xét là liên tục cả, nhưng đều tuyến tính trên từng đoạn.

⌊ x ⌋

{\displaystyle \lfloor x\rfloor }

và

⌈ x ⌉

{\displaystyle \lceil x\rceil }

là hàm hằng trên từng đoạn và gián đoạn tại các điểm nguyên. Hàm

{ x }

{\displaystyle \{x\}}

cũng gián đoạn tại các điểm nguyên, và

mod

{\displaystyle x\,{\bmod {\,}}y}

$x\,{\bmod {\,}}y$ với biến x hằng y gián đoạn tại các bội của y.

⌊ x ⌋

{\displaystyle \lfloor x\rfloor }

là bán liên tục trên còn

⌈ x ⌉

{\displaystyle \lceil x\rceil }

và

{ x }

{\displaystyle \{x\}\;}

$\{x\}\;$ là bán liên tục dưới. x mod y là bán liên tục dưới với y dương và là bán liên tục trên với y âm.

Khai triển chuỗi

Các hàm tất cả chúng ta đang xét đều không liên tục cho nên vì thế chúng không có các khai triển chuỗi lũy thừa. Hàm floor và ceiling không liên tục nên không có khai triển Fourier .

Với y cố định, x mod y có khai triển Fourier

x mod y = y 2 − y π ∑ k = 1 ∞ sin ⁡ ( 2 π k x y ) k. { \ displaystyle x \, { \ bmod { \, } } y = { \ frac { y } { 2 } } – { \ frac { y } { \ pi } } \ sum _ { k = 1 } ^ { \ infty } { \ frac { \ sin \ left ( { \ frac { 2 \ pi kx } { y } } \ right ) } { k } }. } $x\,{\bmod {\,}}y={\frac {y}{2}}-{\frac {y}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin \left({\frac {2\pi kx}{y}}\right)}{k}}.$

Phần lẻ {x} = x mod 1 khai triển:

{ x } = 1 2 − 1 π ∑ k = 1 ∞ sin ⁡ ( 2 π k x ) k. { \ displaystyle \ { x \ } = { \ frac { 1 } { 2 } } – { \ frac { 1 } { \ pi } } \ sum _ { k = 1 } ^ { \ infty } { \ frac { \ sin ( 2 \ pi kx ) } { k } }. } $\{x\}={\frac {1}{2}}-{\frac {1}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin(2\pi kx)}{k}}.$

sử dụng công thức { x } = x − floor ( x ), floor ( x ) = x − { x } ta có

⌊ x ⌋ = x − 1 2 + 1 π ∑ k = 1 ∞ sin ⁡ ( 2 π k x ) k. { \ displaystyle \ lfloor x \ rfloor = x – { \ frac { 1 } { 2 } } + { \ frac { 1 } { \ pi } } \ sum _ { k = 1 } ^ { \ infty } { \ frac { \ sin ( 2 \ pi kx ) } { k } }. } $\lfloor x\rfloor =x-{\frac {1}{2}}+{\frac {1}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin(2\pi kx)}{k}}.$

Hàm phần lẻ là hàm răng cưa, ký hiệu

{ x }

{\displaystyle \{x\}}

với x là số thực, được định nghĩa bởi công thức

{ x } = x − ⌊ x ⌋. { \ displaystyle \ { x \ } = x – \ lfloor x \ rfloor. } $\{x\}=x-\lfloor x\rfloor .$

Với mọi x,

0 ≤ { x } $0\leq \{x\}<1.\;$

Với x>0 trong dạng thập phân, floor(x) là phần bên trái của biểu diễn thập phân, phần lẻ của x là phần bên phải khi thay tất cả các số bên trái bởi 0.

: Phần mềm SPSS là gì? Tìm hiểu chức năng và ứng dụng của SPSS

Toán tử mod

Toán tử mod, ký hiệu là x mod y,x, y thực, y ≠ 0, xác định theo công thức

x mod y = x − y ⌊ x y ⌋. { \ displaystyle x \, { \ bmod { \, } } y = x-y \ left \ lfloor { \ frac { x } { y } } \ right \ rfloor. }

x mod y luôn nằm giữa 0 và y; i.e.

Nếu y > 0,

0 ≤ x

mod

y $0\leq x\,{\bmod {\,}}y<y,$

còn nếu y

0 ≥ x mod y > y. { \ displaystyle 0 \ geq x \, { \ bmod { \, } } y > y. } ${\displaystyle 0\geq x\,{\bmod {\,}}y>y.}” class=”mwe-math-fallback-image-inline” src=”https://wikimedia.org/api/rest_v1/media/math/render/svg/afa0a828d199d249f097649054e8a549903f173b”/></dd> </dl> Nếu x nguyên còn y nguyên dương, <dl> <dd><span class=$ ( x mod y ) ≡ x ( mod y ). { \ displaystyle ( x \, { \ bmod { \, } } y ) \ equiv x { \ pmod { y } }. } $(x\,{\bmod {\,}}y)\equiv x{\pmod {y}}.$

x mod y với y có định là hàm răng cưa.

Gauss’s third proof of quadratic reciprocity, as modified by Eisenstein, has two basic steps.

Let p and q be distinct positive odd prime numbers, and let

m = p − 1 2, n = q − 1 2. { \ displaystyle m = { \ frac { p-1 } { 2 } }, \ ; \ ; n = { \ frac { q-1 } { 2 } }. } $m={\frac {p-1}{2}},\;\;n={\frac {q-1}{2}}.$

First, Gauss’s lemma is used to show that the Legendre symbols are given by

( q p ) = ( − 1 ) ⌊ q p ⌋ + ⌊ 2 q p ⌋ + ⋯ + ⌊ m q p ⌋ { \ displaystyle \ left ( { \ frac { q } { p } } \ right ) = ( – 1 ) ^ { \ left \ lfloor { \ frac { q } { p } } \ right \ rfloor + \ left \ lfloor { \ frac { 2 q } { p } } \ right \ rfloor + \ dots + \ left \ lfloor { \ frac { mq } { p } } \ right \ rfloor } } $\left({\frac {q}{p}}\right)=(-1)^{\left\lfloor {\frac {q}{p}}\right\rfloor +\left\lfloor {\frac {2q}{p}}\right\rfloor +\dots +\left\lfloor {\frac {mq}{p}}\right\rfloor }$

and

( p q ) = ( − 1 ) ⌊ p q ⌋ + ⌊ 2 p q ⌋ + ⋯ + ⌊ n p q ⌋. { \ displaystyle \ left ( { \ frac { p } { q } } \ right ) = ( – 1 ) ^ { \ left \ lfloor { \ frac { p } { q } } \ right \ rfloor + \ left \ lfloor { \ frac { 2 p } { q } } \ right \ rfloor + \ dots + \ left \ lfloor { \ frac { np } { q } } \ right \ rfloor }. } $\left({\frac {p}{q}}\right)=(-1)^{\left\lfloor {\frac {p}{q}}\right\rfloor +\left\lfloor {\frac {2p}{q}}\right\rfloor +\dots +\left\lfloor {\frac {np}{q}}\right\rfloor }.$

The second step is to use a geometric argument to show that

⌊ q p ⌋ + ⌊ 2 q p ⌋ + ⋯ + ⌊ m q p ⌋ + ⌊ p q ⌋ + ⌊ 2 p q ⌋ + ⋯ + ⌊ n p q ⌋ = m n. { \ displaystyle \ left \ lfloor { \ frac { q } { p } } \ right \ rfloor + \ left \ lfloor { \ frac { 2 q } { p } } \ right \ rfloor + \ dots + \ left \ lfloor { \ frac { mq } { p } } \ right \ rfloor + \ left \ lfloor { \ frac { p } { q } } \ right \ rfloor + \ left \ lfloor { \ frac { 2 p } { q } } \ right \ rfloor + \ dots + \ left \ lfloor { \ frac { np } { q } } \ right \ rfloor = mn. } $\left\lfloor {\frac {q}{p}}\right\rfloor +\left\lfloor {\frac {2q}{p}}\right\rfloor +\dots +\left\lfloor {\frac {mq}{p}}\right\rfloor +\left\lfloor {\frac {p}{q}}\right\rfloor +\left\lfloor {\frac {2p}{q}}\right\rfloor +\dots +\left\lfloor {\frac {np}{q}}\right\rfloor =mn.$

Combining these formulas gives quadratic reciprocity in the form

( p q ) ( q p ) = ( − 1 ) m n = ( − 1 ) p − 1 2 q − 1 2. { \ displaystyle \ left ( { \ frac { p } { q } } \ right ) \ left ( { \ frac { q } { p } } \ right ) = ( – 1 ) ^ { mn } = ( – 1 ) ^ { { \ frac { p-1 } { 2 } } { \ frac { q-1 } { 2 } } }. } $\left({\frac {p}{q}}\right)\left({\frac {q}{p}}\right)=(-1)^{mn}=(-1)^{{\frac {p-1}{2}}{\frac {q-1}{2}}}.$

There are formulas that use floor to express the quadratic character of small numbers mod odd primes p:

( 2 p ) = ( − 1 ) ⌊ p + 1 4 ⌋, { \ displaystyle \ left ( { \ frac { 2 } { p } } \ right ) = ( – 1 ) ^ { \ left \ lfloor { \ frac { p + 1 } { 4 } } \ right \ rfloor }, } $\left({\frac {2}{p}}\right)=(-1)^{\left\lfloor {\frac {p+1}{4}}\right\rfloor },$

( 3 p ) = ( − 1 ) ⌊ p + 1 6 ⌋. { \ displaystyle \ left ( { \ frac { 3 } { p } } \ right ) = ( – 1 ) ^ { \ left \ lfloor { \ frac { p + 1 } { 6 } } \ right \ rfloor }. } $\left({\frac {3}{p}}\right)=(-1)^{\left\lfloor {\frac {p+1}{6}}\right\rfloor }.$

Việc làm tròn các số dương x đến số nguyên gần nhất được diễn tả như sau

⌊ x + 0.5 ⌋ .

{\displaystyle \lfloor x+0.5\rfloor .}

$\lfloor x+0.5\rfloor .$

Số các chữ số

Số các chữ số trong hệ cơ số b của số nguyên dương k là

⌊ log b ⁡ k ⌋ + 1. { \ displaystyle \ lfloor \ log _ { b } { k } \ rfloor + 1. } $\lfloor \log _{b}{k}\rfloor +1.$

Thừa số của giai thừa

đặt n nguyên dương và p là số nguyên tố. Lũy thừa của p trong khai triển của n! được cho bởi công thức

⌊ n p ⌋ + ⌊ n p 2 ⌋ + ⌊ n p 3 ⌋ + … { \ displaystyle \ left \ lfloor { \ frac { n } { p } } \ right \ rfloor + \ left \ lfloor { \ frac { n } { p ^ { 2 } } } \ right \ rfloor + \ left \ lfloor { \ frac { n } { p ^ { 3 } } } \ right \ rfloor + \ dots } $\left\lfloor {\frac {n}{p}}\right\rfloor +\left\lfloor {\frac {n}{p^{2}}}\right\rfloor +\left\lfloor {\frac {n}{p^{3}}}\right\rfloor +\dots$

Chú ý rằng đó là tổng có giới hạn, số hạng bằng không khi pk >n.

Beatty sequence shows how every positive irrational number gives rise to a partition of the natural numbers into two sequences via the floor function.

Hằng số Euler γ

Đây là các công thức cho Hằng số Euler γ = 0.57721 56649 … chứa các hàm floor và ceiling, e. g.

γ = ∫ 1 ∞ ( 1 ⌊ x ⌋ − 1 x ) d x, { \ displaystyle \ gamma = \ int _ { 1 } ^ { \ infty } \ left ( { 1 \ over \ lfloor x \ rfloor } – { 1 \ over x } \ right ) \, dx, } $\gamma =\int _{1}^{\infty }\left({1 \over \lfloor x\rfloor }-{1 \over x}\right)\,dx,$

γ = lim n → ∞ 1 n ∑ k = 1 n ( ⌈ n k ⌉ − n k ), { \ displaystyle \ gamma = \ lim _ { n \ to \ infty } { \ frac { 1 } { n } } \, \ sum _ { k = 1 } ^ { n } \ left ( \ left \ lceil { \ frac { n } { k } } \ right \ rceil – { \ frac { n } { k } } \ right ), } $\gamma =\lim _{n\to \infty }{\frac {1}{n}}\,\sum _{k=1}^{n}\left(\left\lceil {\frac {n}{k}}\right\rceil -{\frac {n}{k}}\right),$

và

γ = ∑ k = 2 ∞ ( − 1 ) k ⌊ log 2 ⁡ k ⌋ k = 1 2 − 1 3 + 2 ( 1 4 − 1 5 + 1 6 − 1 7 ) + 3 ( 1 8 − ⋯ − 1 15 ) + … { \ displaystyle \ gamma = \ sum _ { k = 2 } ^ { \ infty } ( – 1 ) ^ { k } { \ frac { \ left \ lfloor \ log _ { 2 } k \ right \ rfloor } { k } } = { \ tfrac { 1 } { 2 } } – { \ tfrac { 1 } { 3 } } + 2 \ left ( { \ tfrac { 1 } { 4 } } – { \ tfrac { 1 } { 5 } } + { \ tfrac { 1 } { 6 } } – { \ tfrac { 1 } { 7 } } \ right ) + 3 \ left ( { \ tfrac { 1 } { 8 } } – \ dots – { \ tfrac { 1 } { 15 } } \ right ) + \ dots } $\gamma =\sum _{k=2}^{\infty }(-1)^{k}{\frac {\left\lfloor \log _{2}k\right\rfloor }{k}}={\tfrac {1}{2}}-{\tfrac {1}{3}}+2\left({\tfrac {1}{4}}-{\tfrac {1}{5}}+{\tfrac {1}{6}}-{\tfrac {1}{7}}\right)+3\left({\tfrac {1}{8}}-\dots -{\tfrac {1}{15}}\right)+\dots$

Hàm Riemann ζ

Các công thức cho số nguyên tố

n là số nguyên tố khi và chỉ khi[16]

∑ m = 1 ∞ ( ⌊ n m ⌋ − ⌊ n − 1 m ⌋ ) = 2. { \ displaystyle \ sum _ { m = 1 } ^ { \ infty } \ left ( \ left \ lfloor { \ frac { n } { m } } \ right \ rfloor – \ left \ lfloor { \ frac { n-1 } { m } } \ right \ rfloor \ right ) = 2. } $\sum _{m=1}^{\infty }\left(\left\lfloor {\frac {n}{m}}\right\rfloor -\left\lfloor {\frac {n-1}{m}}\right\rfloor \right)=2.$

r là số nguyên lớn hơn 1, pn là số nguyên tố thứ n, ký hiệu

α = ∑ m = 1 ∞ p m r − m 2. { \ displaystyle \ alpha = \ sum _ { m = 1 } ^ { \ infty } p_ { m } r ^ { – m ^ { 2 } }. } $\alpha =\sum _{m=1}^{\infty }p_{m}r^{-m^{2}}.$

Thì [ 17 ]

p n = ⌊ r n 2 α ⌋ − r 2 n − 1 ⌊ r ( n − 1 ) 2 α ⌋. { \ displaystyle p_ { n } = \ left \ lfloor r ^ { n ^ { 2 } } \ alpha \ right \ rfloor – r ^ { 2 n – 1 } \ left \ lfloor r ^ { ( n-1 ) ^ { 2 } } \ alpha \ right \ rfloor. } $p_{n}=\left\lfloor r^{n^{2}}\alpha \right\rfloor -r^{2n-1}\left\lfloor r^{(n-1)^{2}}\alpha \right\rfloor .$

Có số θ = 1.3064 … với đặc thù

⌊ θ 3 ⌋, ⌊ θ 9 ⌋, ⌊ θ 27 ⌋, … { \ displaystyle \ left \ lfloor \ theta ^ { 3 } \ right \ rfloor, \ left \ lfloor \ theta ^ { 9 } \ right \ rfloor, \ left \ lfloor \ theta ^ { 27 } \ right \ rfloor, \ dots } $\left\lfloor \theta ^{3}\right\rfloor ,\left\lfloor \theta ^{9}\right\rfloor ,\left\lfloor \theta ^{27}\right\rfloor ,\dots$

đều là số nguyên tố. [ 18 ]Cũng có thêm số ω = 1.9287800 … mà

⌊ 2 ω ⌋, ⌊ 2 2 ω ⌋, ⌊ 2 2 2 ω ⌋, … { \ displaystyle \ left \ lfloor 2 ^ { \ omega } \ right \ rfloor, \ left \ lfloor 2 ^ { 2 ^ { \ omega } } \ right \ rfloor, \ left \ lfloor 2 ^ { 2 ^ { 2 ^ { \ omega } } } \ right \ rfloor, \ dots } $\left\lfloor 2^{\omega }\right\rfloor ,\left\lfloor 2^{2^{\omega }}\right\rfloor ,\left\lfloor 2^{2^{2^{\omega }}}\right\rfloor ,\dots$

đều nguyên tố. [ 18 ]

π(x) là số các số nguyên tố nhỏ hơn hoặc bằng x. Nó được suy luận từ Định lý Wilson[19]

π ( n ) = ∑ j = 2 n ⌊ ( j − 1 ) ! + 1 j − ⌊ ( j − 1 ) ! j ⌋ ⌋. { \ displaystyle \ pi ( n ) = \ sum _ { j = 2 } ^ { n } \ left \ lfloor { \ frac { ( j-1 ) ! + 1 } { j } } – \ left \ lfloor { \ frac { ( j-1 ) ! } { j } } \ right \ rfloor \ right \ rfloor. } $\pi (n)=\sum _{j=2}^{n}\left\lfloor {\frac {(j-1)!+1}{j}}-\left\lfloor {\frac {(j-1)!}{j}}\right\rfloor \right\rfloor .$

Nếu n ≥ 2,[20]

π ( n ) = ∑ j = 2 n ⌊ 1 ∑ k = 2 j ⌊ ⌊ j k ⌋ k j ⌋ ⌋. { \ displaystyle \ pi ( n ) = \ sum _ { j = 2 } ^ { n } \ left \ lfloor { \ frac { 1 } { \ sum _ { k = 2 } ^ { j } \ left \ lfloor \ left \ lfloor { \ frac { j } { k } } \ right \ rfloor { \ frac { k } { j } } \ right \ rfloor } } \ right \ rfloor. } $\pi (n)=\sum _{j=2}^{n}\left\lfloor {\frac {1}{\sum _{k=2}^{j}\left\lfloor \left\lfloor {\frac {j}{k}}\right\rfloor {\frac {k}{j}}\right\rfloor }}\right\rfloor .$

Không công thức nào trên đây ứng dụng trong thực tiễn .

Vấn đề đã xử lý

Ramanujan đã gửi các bài toán sau đây đến Journal of the Indian Mathematical Society.[21]

Cho n là số nguyên dương, chứng minh rằng:

⌊ n 3 ⌋ + ⌊ n + 2 6 ⌋ + ⌊ n + 4 6 ⌋ = ⌊ n 2 ⌋ + ⌊ n + 3 6 ⌋, { \ displaystyle \ left \ lfloor { \ tfrac { n } { 3 } } \ right \ rfloor + \ left \ lfloor { \ tfrac { n + 2 } { 6 } } \ right \ rfloor + \ left \ lfloor { \ tfrac { n + 4 } { 6 } } \ right \ rfloor = \ left \ lfloor { \ tfrac { n } { 2 } } \ right \ rfloor + \ left \ lfloor { \ tfrac { n + 3 } { 6 } } \ right \ rfloor, } $\left\lfloor {\tfrac {n}{3}}\right\rfloor +\left\lfloor {\tfrac {n+2}{6}}\right\rfloor +\left\lfloor {\tfrac {n+4}{6}}\right\rfloor =\left\lfloor {\tfrac {n}{2}}\right\rfloor +\left\lfloor {\tfrac {n+3}{6}}\right\rfloor ,$

⌊ 1 2 + n + 1 2 ⌋ = ⌊ 1 2 + n + 1 4 ⌋, { \ displaystyle \ left \ lfloor { \ tfrac { 1 } { 2 } } + { \ sqrt { n + { \ tfrac { 1 } { 2 } } } } \ right \ rfloor = \ left \ lfloor { \ tfrac { 1 } { 2 } } + { \ sqrt { n + { \ tfrac { 1 } { 4 } } } } \ right \ rfloor, } $\left\lfloor {\tfrac {1}{2}}+{\sqrt {n+{\tfrac {1}{2}}}}\right\rfloor =\left\lfloor {\tfrac {1}{2}}+{\sqrt {n+{\tfrac {1}{4}}}}\right\rfloor ,$

⌊ n + n + 1 ⌋ = ⌊ 4 n + 2 ⌋. { \ displaystyle \ left \ lfloor { \ sqrt { n } } + { \ sqrt { n + 1 } } \ right \ rfloor = \ left \ lfloor { \ sqrt { 4 n + 2 } } \ right \ rfloor. } $\left\lfloor {\sqrt {n}}+{\sqrt {n+1}}\right\rfloor =\left\lfloor {\sqrt {4n+2}}\right\rfloor .$

Vấn đề chưa xử lý

Có số nguyên dương k nào thỏa mãn, k ≥ 6, mà:[22]

3 k − 2 k ⌊ ( 3 2 ) k ⌋ > 2 k − ⌊ ( 3 2 ) k ⌋ − 2 ? { \ displaystyle 3 ^ { k } – 2 ^ { k } \ left \ lfloor \ left ( { \ tfrac { 3 } { 2 } } \ right ) ^ { k } \ right \ rfloor > 2 ^ { k } – \ left \ lfloor \ left ( { \ tfrac { 3 } { 2 } } \ right ) ^ { k } \ right \ rfloor – 2 \ ; \ ; ? } ${\displaystyle 3^{k}-2^{k}\left\lfloor \left({\tfrac {3}{2}}\right)^{k}\right\rfloor >2^{k}-\left\lfloor \left({\tfrac {3}{2}}\right)^{k}\right\rfloor -2\;\;?}” class=”mwe-math-fallback-image-inline” src=”https://wikimedia.org/api/rest_v1/media/math/render/svg/a94e1e43891eee9e91fb10d257918a88ecca3b93″/></dd> </dl> Mahler[23] đã chứng minh chỉ có hữu hạn số k như vậy; tuy vậy người ta vẫn chưa biết số nào như vậy. <ol class=$ ^ Lemmermeyer, pp. 10, 23 ^ e. g. Cassels, Hardy và Wright, and Ribenboim use Gauss’s notation, Graham, Knuth và Patashnik, and Crandall và Pomerance use Iverson’s ^ Higham, p. 25 ^ Iverson ^ Graham, Knuth, và Patashink, Ch. 3 ^ Graham, Knuth, và Patashnik, p. 85 and Ex. 3.15 ^ Graham, Knuth, và Patashnik, Ex. 3.12 ^ Titchmarsh, p. 15, Eq. 2.1.7 ^ Graham, Knuth, và Patashnik, p. 70 ^ Lemmermeyer, § 1.4, Ex. 1.32 – 1.33 ^ Hardy và Wright, § § 6.11 – 6.13 ^ Lemmermeyer, p. 25 ^ Hardy và Wright, Th. 416 ^ Graham, Knuth, và Patashnik, pp. 77 – 78 ^Thes e formulas are from the Wikipedia article Euler’s constant, which has many more .^ Crandall và Pomerance, Ex. 1.3, p. 46 ^ Hardy và Wright, § 22.3 ^ ab Ribenboim, p. 186 ^ Ribenboim, p. 181 ^

Crandall & Pomerance, Ex. 1.4, p. 46

Ramanujan, Question 723, Papers p. 332

^ Hardy và Wright, p. 337 ^

Mahler, K. On the fractional parts of the powers of a rational number II, 1957, Mathematika, 4, pages 122-124

Štefan Porubský, “Integer rounding functions”, Interactive Information Portal for Algorithmic Mathematics, Institute of Computer Science of the Czech Academy of Sciences, Prague, Czech Republic, retrieved 10/24/2008