Vành nghĩa là gì? – Wikipedia tiếng Việt

0 Shares

Đối với những định nghĩa khác, xem Vành ( khuynh hướng )

Trong toán học, vành là một trong những cấu trúc đại số cơ bản. Nhiều đối tượng toán học có thể được xem xét như là vành, ví dụ như vành những hàm số liên tục trên một không gian, vành những đa thực một ẩn với hệ số thực, vành những ma trận với hệ số thực, vân vân. Vành có nhiều thuộc tính hơn là nhóm, nhưng lại ít thuộc tính hơn trường, nên nó có một vị trí cân bằng đặc biệt giữa những ngành của toán học.

Một vành hoàn toàn có thể là giao hoán hoặc không giao hoán, tùy thuộc xem phép nhân của nó có tính giao hoán hay không. Các vành giao hoán có một vị trí đặc biệt quan trọng trong triết lý số và hình học đại số. Ngành nghiên cứu và điều tra về những vành giao hoán và những i-đê-an trên vành giao hoán được gọi là đại số giao hoán .

Các vành (không giao hoán) là những đối tượng nghiên cứu quan trọng trong đại số trừu tượng.

Bạn đang đọc: Vành nghĩa là gì? – Wikipedia tiếng Việt

Vành nghĩa là gì? – Wikipedia tiếng Việt

Một tập hợp khác rỗng R được gọi là vành nếu trên đó có hai luật hợp thành trong R mà ta ký hiệu là “+” (phép cộng) và “×” (phép nhân) thoả mãn những điều kiện sau:

R là một nhóm giao hoán đối với phép cộng, nghĩa là: Phép cộng có tính kết hợp: ∀ x, y, z ∈ R : ( x + y ) + z = x + ( y + z ) { \ displaystyle \ forall x, y, z \ in R : ( x + y ) + z = x + ( y + z ) \, } $\forall x,y,z\in R:(x+y)+z=x+(y+z)\,$ Phép cộng có phần tử trung hòa, nghĩa là ∃ 0 ∈ R, ∀ x ∈ R { \ displaystyle \ exists 0 \ in R, \ forall x \ in R } $\exists 0\in R,\forall x\in R$ 0 + x = x + 0 = x { \ displaystyle 0 + x = x + 0 = x \, } $0+x=x+0=x\,$ Mọi phần tử của R có phần tử đối: ∀ x, ∃ x ′ : x + x ′ = x ′ + x = 0 { \ displaystyle \ forall x, \ exists x ‘ : x + x ‘ = x ‘ + x = 0 } $\forall x,\exists x`:x+x`=x`+x=0$ Phép cộng có tính giao hoán, nghĩa là: ∀ x, y ∈ R : x + y = y + x { \ displaystyle \ forall x, y \ in R : x + y = y + x } $\forall x,y\in R:x+y=y+x$ Phép nhân có tính phân phối với phép cộng, nghĩa là ∀ x, y, z ∈ R : x. ( y + z ) = x. y + x. z { \ displaystyle \ forall x, y, z \ in R : x. ( y + z ) = x. y + x. z } $\forall x,y,z\in R:x.(y+z)=x.y+x.z$ Phép nhân có tính kết hợp, nghĩa là ∀ x, y, z ∈ R : ( x. y ). z = x. ( y. z ) { \ displaystyle \ forall x, y, z \ in R : ( x. y ). z = x. ( y. z ) \, } $\forall x,y,z\in R:(x.y).z=x.(y.z)\,$ Phép nhân có phần tử đơn vị, nghĩa là ∃ 1 ∈ R, ∀ x ∈ R : 1. x = x. 1 = x { \ displaystyle \ exists 1 \ in R, \ forall x \ in R : 1. x = x. 1 = x \, } $\exists 1\in R,\forall x\in R:1.x=x.1=x\,$

Tuy nhiên, có trường phái khác, định nghĩa một vành không có điều kiện phép nhân phải có phần tử đơn vị. Trong trường phái này, vành có phần tử đơn vị được gọi là vành có đơn vị.

Nhiều trường phái cho rằng vành không cần tính chất phần tử đơn vị và không cần tính chất kết hợp trong phép nhân. Thí dụ, những loại vành Lie được gọi là vành nhưng phép nhân không có tính chất kết hợp. Người theo trường phái này sử dụng chữ vành kết hợp để gọi một vành trong đó phép nhân có tính kết hợp và để phân biệt giữa hai vành kết hợp và vành không kết hợp.

Một số loại vành đặc biệt quan trọng

Vành giao hoán là vành R trong đó phép nhân có tính chất giao hoán.Vành trong đó phép nhân có phần tử đơn vị được gọi là vành có đơn vị.Nếu trong vành R tồn tại hai phần tử a ≠ 0, b ≠ 0 { \ displaystyle a \ neq 0, b \ neq 0 } $a\neq 0,b\neq 0$ ab = 0 thì những phần tử a, b được gọi là ước của 0 hay nói phương pháp khác 0 ⋮ a, 0 ⋮ b. { \ displaystyle 0 \ \ vdots \ a, \ 0 \ \ vdots \ b. } $0\ \vdots \ a,\ 0\ \vdots \ b.$ miền nguyên.Miền nguyên X gọi là vành chính nếu mọi ideal của nó đều là được sinh từ một phần tử (tức là mọi ideal của nó đều là ideal chính).Miền nguyên A gọi là vành Euclid nếu có ánh xạ f: Ā→N (với Ā là tập những phần tử khác 0 của A) thoả mãn tính chất sau: Nếu b là ước của a và a ≠ 0 thì f(b) ≤ f(a).Với a, b là hai phần tử tuỳ ý của A và b ≠ 0 thì tồn tại duy nhất cặp phần tử q, r của A sao cho a = bq + r và f(b) ≥ f(r) nếu r ≠ 0. Có ví dụ như mọi vành đa thức là vành Ơclit.Vành Noether: Vành giao hoán có đơn vị được gọi là vành Noether nếu mọi ideal của nó đều là hữu hạn sinh, tức là tồn tại một tập sinh hữu hạn phần tử. Định lý – Một vành là Noether khi và chỉ khi nó thỏa mãn điều kiện dãy tăng.Chứng minh – Giả sử một vành A thỏa mãn điều kiện dãy tăng. Giả sử tồn tại một i-đê-an I { \ displaystyle I }( x i ) i ∈ N { \ displaystyle ( x_ { i } ) _ { i \ in \ mathbb { N } } } $(x_{i})_{i\in \mathbb {N} }$ I { \ displaystyle I }x n + 1 ∉ ( x 1, …, x n ) { \ displaystyle x_ { n + 1 } \ notin ( x_ { 1 }, \ dots, x_ { n } ) } $x_{n+1}\notin (x_{1},\dots ,x_{n})$ ( x 1 ) ⊂ ( x 1, x 2 ) ⊂ … { \ displaystyle ( x_ { 1 } ) \ subset ( x_ { 1 }, x_ { 2 } ) \ subset \ dots } $(x_{1})\subset (x_{1},x_{2})\subset \dots$ A { \ displaystyle A }Ngược lại, giả sử vành mọi i-đê-an trong vành A đều là hữu hạn sinh. Xét một dãy tăng những i-đê-an I 1 ⊂ I 2 ⊂ … { \ displaystyle I_ { 1 } \ subset I_ { 2 } \ subset \ dots } $I_{1}\subset I_{2}\subset \dots$ I = ∪ i ∈ N I i { \ displaystyle I = \ cup _ { i \ in \ mathbb { N } } I_ { i } } $I=\cup _{i\in \mathbb {N} }I_{i}$ I { \ displaystyle I }x 1, …, x n { \ displaystyle x_ { 1 }, \ dots, x_ { n } } $x_{1},\dots ,x_{n}$ I = ( x 1, …, x n ) { \ displaystyle I = ( x_ { 1 }, \ dots, x_ { n } ) } $I=(x_{1},\dots ,x_{n})$ j { \ displaystyle j } $j$ x j ∈ ∪ i ∈ N I i { \ displaystyle x_ { j } \ in \ cup _ { i \ in \ mathbb { N } } I_ { i } } $x_{j}\in \cup _{i\in \mathbb {N} }I_{i}$ ∃ m j : x j ∈ I m j { \ displaystyle \ exists m_ { j } : x_ { j } \ in I_ { m_ { j } } } $\exists m_{j}:x_{j}\in I_{m_{j}}$ m = max m 1, …, m n { \ displaystyle m = \ max { m_ { 1 }, \ dots, m_ { n } } } $m=\max {m_{1},\dots ,m_{n}}$ I m { \ displaystyle I_ { m } } $I_{m}$ A thỏa mãn điều kiện dãy tăng.Vành Gauss hay vành nhân tử hoá là một miền nguyên A mà mọi phần tử khác không và không khả nghịch đều được phân tích một phương pháp duy nhất thành tích của hữu hạn phần tử bất khả quy nếu không tính đến thứ tự của những phần tử (duy nhất xê xích một hoán vị).Tập hợp những số nguyên Z { \ displaystyle \ mathbb { Z } } $\mathbb {Z}$ Tập những ma trận vuông cùng cấp n với phép cộng và nhân ma trận là một vành.Tập những đa thức với hệ số trên trường số thực là một vành.Tập những số dạng a + b. 3 { \ displaystyle a + b. { \ sqrt { 3 } } } $a+b.{\sqrt {3}}$ a, b ∈ Z { \ displaystyle a, b \ in \ mathbb { Z } } $a,b\in \mathbb {Z}$ Vành số nguyên với phép toán cộng và nhân thông thường là vành Euclid, vành chính,và vành Gauss.Các vành chính, vành Euclid, vành đa thức trên một trường K là những vành Gauss.

Một số nguyên Gauss (hay số nguyên phức) là một số phức mà những phần thực và phần ảo của nó là những số nguyên. Các số nguyên Gauss, với phép toán cộng và phép toán nhân những số phức tạo thành một vành, gọi là vành số nguyên Gauss, thường ký hiệu là Z[i].

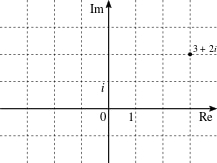Các số nguyên Gauss như những điểm mắt lưới trên mặt phẳng phức .

Trong vành số nguyên Gauss, ta cũng có thể xây dựng những khái niệm tương tự như trong vành số nguyên như: chia hết, số nguyên tố Gauss, đồng dư,… Khái niệm đóng vai trò quan trọng đối với những số nguyên Gauss là chuẩn của số nguyên Gauss được định nghĩa là:

‖ a + b . i ‖ =

{\displaystyle \|a+b.i\|=a^{2}+b^{2}}

$\|a+b.i\|=a^{2}+b^{2}$ . Có những kết quả khá thú vị như: nếu

‖ Z ‖

{\displaystyle \|Z\|}

$\|Z\|$ là số nguyên tố thì Z là số nguyên tố Gauss.

Tập con A của vành R được gọi là vành con của R nếu chính A là một vành với hai phép toán cộng và nhân trên R (bao gồm cả tính đóng của hai phép toán này trên A.

Các vành con đặc biệt: Tập gồm một phần tử {0}, và chính R là vành con của RCho phần tử a∈ { \ displaystyle \ in } $\in$ R. Tập những phần tử dạng n.a,

n ∈

{\displaystyle n\in \mathbb {Z} }

$n\in \mathbb {Z}$ R

Các điều kiện kèm theo tương tự

Cho R là một vành, tập con A

⊂

{\displaystyle \subset }

$\subset$ R. Các mệnh đề sau là tương đương:

A là vành con của R;∀ { \ displaystyle \ forall } $\forall$ ∈ { \ displaystyle \ in }A, x ± y∈ { \ displaystyle \ in }A, x.y∈ { \ displaystyle \ in }A, –x và –y∈ { \ displaystyle \ in }A.

Giao của những vành con

Giao của họ bất kỳ những vành con của R là vành con của R

Các khái niệm

Vành con A của vành R được gọi là ideal trái (hoặc phải) của R nếu x. a ∈ A { \ displaystyle x. a \ in A } $x.a\in A$ a. x ∈ A { \ displaystyle a. x \ in A } $a.x\in A$ ∀ a ∈ A, x ∈ R { \ displaystyle \ forall a \ in A, x \ in R } $\forall a\in A,x\in R$ Vành con A vừa là ideal trái, vừa là ideal phải của R được gọi là ideal của R.Giao của họ bất kỳ những ideal của R là ideal của R.Cho tập con X ⊂ R { \ displaystyle X \ subset R } $X\subset R$ R chứa X được gọi là ideal sinh bởi X.Giả sử A là vành giao hoán có đơn vị,một ideal X⊂ { \ displaystyle \ subset }Ideal P của A gọi là ideal nguyên tố nếu và chỉ nếu tích uv thuộc P thì u∈ { \ displaystyle \ in }∈ { \ displaystyle \ in }Mọi ideal là vành con, ngược lại chưa chắc đúng.

Một số tác dụng

Nếu R là vành giao hoán, có đơn vị thì iđean sinh bởi tập con của R:{a1,a2,…,ak}

là tập hợp những thành phần dạng :

a1.x1+a2.x2+…+ak.xk

trong đó x1,x2,…,xk

∈

{\displaystyle \in }

Nếu R là vành có đơn vị của R và A là ideal của R chứa đơn vị thì A=R.Tập ℕ, ℤ và những tập con của nó đều không phải là những ideal của tập số thực.Cho A là một ideal của vành R và phần tử x∈ { \ displaystyle \ in }R.Tập con của R gồm những phần tử dạng x+a với mọi a∈ { \ displaystyle \ in }A được gọi là một lớp kề của A theo x.Ký hiệu R/A là tập hợp tất cả những lớp kề của A với mọi x∈ { \ displaystyle \ in }R:R / A = { x + A | x ∈ R } { \ displaystyle R / A = \ { x + A | x \ in R \ } } $R/A=\{x+A|x\in R\}$ được gọi là tập thương của R theo A.Trên tập thương R/A có thể xác định hai phép toán cộng và nhân như sau: (x+A)+(y+A)=(x+y)+A(x+A).(y+A)=(x.y)+A

Khi đó có thể chứng minh R/A là một vành, vành này được gọi là vành thương của R theo A.

Ví dụ:

Cho n là số nguyên dương. Tập

n .

{\displaystyle n.\mathbb {Z} }

$n.\mathbb {Z}$ là ideal của

{\displaystyle \mathbb {Z} }

. Vành thương

{\displaystyle \mathbb {Z} }

n .

{\displaystyle n.\mathbb {Z} }

chính là vành những lớp đồng dư theo môđun n.

giả sử X là một vành giao hoán có đơn vị và A là một ideal của X khi đó

Đồng cấu vành

Cho R và R là hai vành. Ánh xạ f:R→ { \ displaystyle \ to } $\to$ R được gọi là đồng cấu vành nếu f bảo toàn hai phép toán cộng và nhân trong R, nghĩa là với mọi a,b∈ { \ displaystyle \ in }R:f(a + b) =f(a) + f(b)f(a.b) = f(a).f(b)Nếu đồng cấu f là đơn ánh (hoặc toàn ánh) thì tương ứng f được gọi là đơn cấu vành(hoặc toàn cấu vành).Nếu đồng cấu f là song ánh thì f được gọi là đẳng cấu vành.Nếu R’=R thì f được gọi là tự đồng cấu của vành R.Nếu có đồng cấu (hoặc đẳng cấu)f từ vành R đến vành Rthì R được gọi là đồng cấu (hoặc đẳng cấu) với R.Ánh xạ không f: R \to R’ cho f(x) = 0 với mọi x∈ { \ displaystyle \ in }R là đồng cấu vành.Ánh xạ đồng nhất của R là một tự đồng cấu của R.Cho A là vành con của R. Ánh xạ nhúng j:A→ { \ displaystyle \ to }R cho j(a)=a với mọi a∈ { \ displaystyle \ in }A là một đơn cấu vành. Nó được gọi là đơn cấu chính tắc từ A vào R.Cho A là ideal của R. Ánh xạ h:R→ { \ displaystyle \ to }R/A cho h(x)=x+A là một toàn cấu, nó được gọi là toàn cấu chính tắc.Tích (ánh xạ) của hai đồng cấu là đồng cấu. Tích (ánh xạ) của hai đẳng cấu là đẳng cấu.

Ảnh và hạt nhân của đồng cấu

Khái niệmCho đồng cấu vành f: R→ { \ displaystyle \ to }R’.Tập con của R gồm những phần tử của R có ảnh là phần tử không của R‘ được gọi là hạt nhân của đồng cấu f, ký hiệu là Ker(f)Ker(f)={x∈ { \ displaystyle \ in }R| f(x)=0}Tập f(R) được gọi là ảnh của đồng cấu f, ký hiệu là Im(f).Tính chấtKer(f) là ideal của R và Im(f) là vành con của R’.Đồng cấu f là đơn cấu khi và chỉ khi Ker(f)={0}Với mọi đồng cấu f:R→ { \ displaystyle \ to }R‘, Im(f) đẳng cấu với vành thương R/Ker(f).

Phạm trù những vành

Vành cùng với đồng cấu vành tạo thành phạm trù những vành, được ký hiệu là Ring (từ “vành” trong tiếng Anh). Ring là một phạm trù lớn, cụ thể.

Phạm trù những vành giao hoán được ký hiệu là CRing. CRing tương đương với phạm trù những lược đồ a-phin.

Đặc số của vành

Cho vành có đơn vị R. Nếu tồn tại số nguyên dương m sao cho m.1 = 0 thì số m nhỏ nhất có tính chất đó được gọi là đặc số của R. Nếu không tồn tại m như vậy R được gọi là có đặc số 0.Ví dụ: Vành số nguyên Z { \ displaystyle \ mathbb { Z } }Z { \ displaystyle \ mathbb { Z } }n. Z { \ displaystyle n. \ mathbb { Z } }n.

Sơ lược về lịch sử vẻ vang nghiên cứu và điều tra vành đại số

Những người góp công lớn trong việc nghiên cứu vành đại số và ideal là những nhà toán học Đức mà đại diện là: E. Kummer (1810-1893); R. Dedekin (1831-1936) và đặc biệt là nhà toán học nữ E. Noether (1882-1935). Khi chứng minh bài toán Fermat lớn, E. Kummer đã sử dụng phương pháp xuống thang trên tập số nguyên nhưng mọi cố gắng đều thất bại. Để khắc phục ông đã xét bài toán trong lớp vành thực sự chứa Z. Trên lớp vành này ông phải làm việc với những số ideal là mầm mống của khái niệm ideal sau này.người đưa khái niệm ideal là Dedekin và người có công lớn trong việc phát triển lý thuyết vành và ideal trừu tượng là E. Noether.